introduction
数据结构在设计时考虑了传感器网络,其中最小化无线电传输开销是非常重要的。它最初出现在 “Medians and Beyond: New Aggregation Techniques for Sensor Networks” 由 Shrivastava 等人提出.
example
Q-Digest 只是一个完整的二叉树,在值的范围内,其中叶节点本身就是值。在下面的例子中,我们对包含 1 到 4 的值进行了摘要,我们看到值 1 和值 4 都是 7 次。

新颖性是压缩算法,它允许低频值在树上传播并合并。在下面的例子中,我们有一些信息丢失。我们知道在 1 和 2 之间有 10 个值,但是我们不知道每个值的确切数量

在构建 qdigest 时,要记住一个不变的因素。一个节点,其兄弟和它的父节点的总数必须大于 n / k,其中 n 是所有计数的总和,k 是我们选择的压缩因子。根节点是一个例外。在本文中,这被称为属性 2. 属性 1 指出,除非是叶节点,否则节点的数量必须小于 n / k。在原始文件中使用属性 1 来证明对 qdigest 的一些保证。
requirement
数据结构提供了一些很好的保证,使其非常实用:
给定一个压缩因子 k,摘要的大小不会超过 3k
合并两个 q - 摘要时,如分布式设置中常见的那样,所有必须做的就是将这两个 q - 摘要合并,并运行压缩算法。这比 GK 算法的分布式扩展简单得多。
在回答分位数查询时,误差受 log(σ)/ k 限制,其中σ是存储在摘要中的值的最大范围。因此,我们对中位查询的回答总是在 0.5n 和(0.5 + log(σ)/ k)* n 之间。
合并摘要时,我们可以保持相同的相对错误
正如我们在将来的文章中将会看到的那样,我们可以增加数据结构来创造许多有趣的可能性
论文中的实例
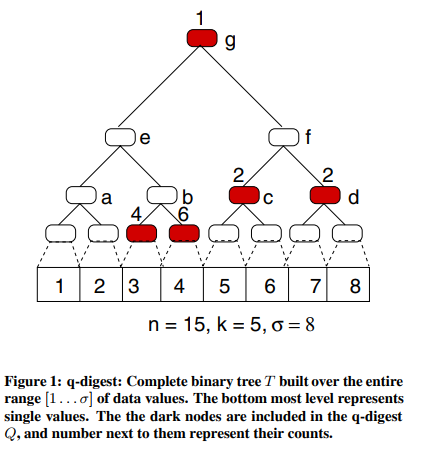
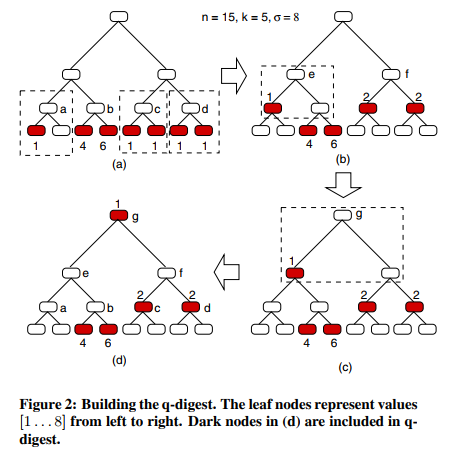
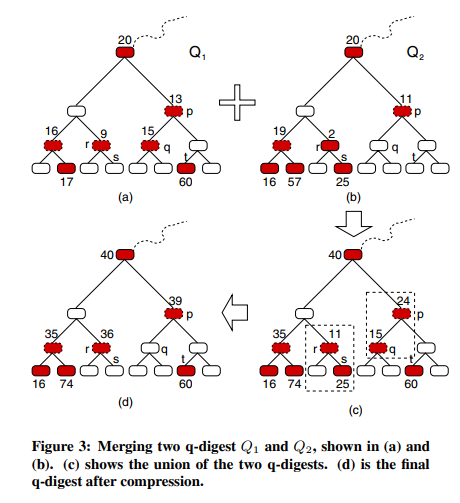
通过这种特殊的数据结构,保持下来的信息具有以下特征,关于经常出现的数据值的详细信息被保存在摘要中,而不经常出现的值被集中到更大的桶中导致信息丢失
papercruncher 的博客 Medians and Beyond: New Aggregation Techniques for Sensor Networks 原文 实现